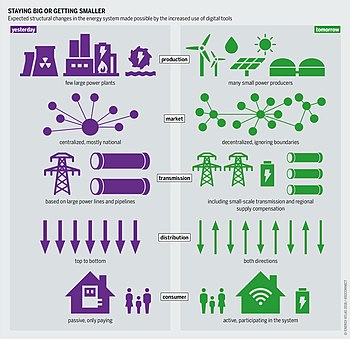
Problem: Real-time control of distributed generation is not a problem, although it requires less human involvement in the management of generators and more fully automated control. However, the integration of distributed power into the backbone grid poses problems related to the dynamic interaction of main grid generators with high inertia with distributed generation, including RES, which have low inertia. As a result of such interaction, there are dangerous low-stable fluctuations, which can lead to the failure of technological equipment of consumers, or electrical equipment in the main network, as well as the development of cascade failure. A new task of monitoring the stability stock for main power grids arises.
Approaches: Modal analysis is the main method of monitoring dangerous fluctuations in the world. Suggested solution: Hybrid method of monitoring the degree of stability of the oscillation group: modal analysis in combination with the sub-gramian method. Gramian is the matrix solution of the matrix Lyapunov equation, which is used in the direct Lyapunov method in the Lyapunov stability criteria for the dynamic system. The sub-gramian is the spectral component of the decomposition of the gramian matrix into the proper numbers of the EES dynamics matrix. This energy can be represented as a sum of positive numbers, each of which determines the energy of a particular mode. It is proved that when the system approaches the stability boundary conditioned by the approximation of the weakly stable mode to the imaginary axis, the Euclidean norm of the matrix of the subgramian of this mode tends to infinity. The physical meaning of this statement is that part of the energy flows into weakly stable modes, which leads to a decrease in the decrement of mode attenuation and to the swaying of the system. Methods of modal analysis and sub-gramianes will complement each other well in the task of monitoring dangerous oscillations, so the combined method using both approaches to stability analysis enhances the advantages of each method and smoothes out disadvantages.
Research methods: Methods of analysis of stability of complex multiresonant dynamic systems - linear and nonlinear systems with smooth nonlinearities, described by ordinary differential equations. It is necessary to know the mathematical model of the power system, which can be restored from the data of measurements of the states of the system.
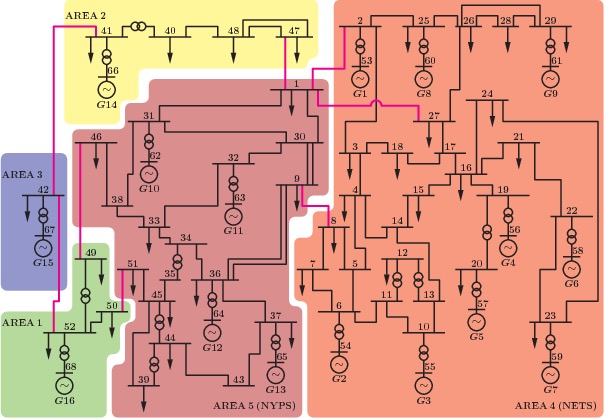
Object of research: Electric power system functioning in normal and emergency mode.
Potential customer: PJSC ROSSETI, Electric Power Industry Development Institutes (EnergyNet)